GRAFIK > GRAPH 4.3

Disini akan membahas pembuatan grafik dengan menggunakan aplikasi Graph 4.3.

A.    Menggambar grafik fungsi sinus & cosinus

Pertama akan membuat grafik sinus, caranya dengan klik Function – Insert Function atau bisa langsung klik pada menubarnya.

Masukkan fungsi (sin) pada kotak seperti gambar dibawah ini. Lalu untuk membuat ketebalan garis supaya lebih terlihat dan mengganti warna garis yang kita inginkan, lihat pada Graph Properties.

Hasilnya.

Sekarang membuat grafik fungsi cosinus. Caranya sama sepeti diatas dengan mengetik cos pada kolom fungsi.

Hasilnya.

Untuk mengetahui daerah antara grafik sinus dan cosines, caranya dengan mengasir garis fungsi dengan mengklik Insert Shading – Between Functions – Ok.

Akan muncul gambar seperti ini, klik Ok lalu klik fungsinya (f(x)= sin x) – Ok.

Hasilnya.

Untuk menghitung luas daerah grafik dari salah satu fungsi, misalnya fungsi sinus. Caranya dengan klik fungsi sin, lalu klik Calculate area.

Akan muncul kotak seperti dibawah ini. Disini yang akan dihitung luas daerah grafik dari 2 sampai 9 dan terdapatnya hasilnya 0,495.

B.     Menggambar Elips.

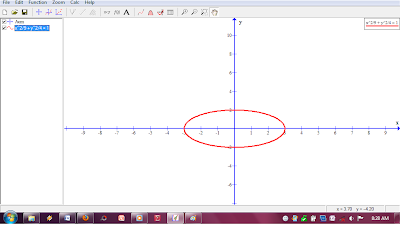
Membuat gambar elips dengan persamaan

Caranya dengan klik Functions – Insert relation.

 

Lalu ketik persamaan elips pada relation x^2/9 + y^2/4 = 1 – Ok .

Hasilnya.

C.    Menggambar Parabola dan Garis Singgung Parabola

Membuat gambar elips dengan persamaan y² = 8x

Caranya dengan klik Functions – Insert relation.

Lalu ketik persamaan parabola pada relation y^2 = 8x – Ok.

Hasilnya.

Sekarang membuat garis singgung dengan titik (2, 4). Disini tidak bisa secara langsung memasukkan titiknya kemudian diperoleh gambar garis singgungnya, tetapi harus dicari dulu persamaan garis.

y y₁ = P (x + x₁)

4y = 4 (x + 2)

4y = 4x + 8

y = x + 2

Setelah kita mendapatkan persamaan garis singgung pada parabola. Masukkan fungsi persamaan garis pada kotak seperti gambar diatas tadi.

Hasilnya.

 Sekian. terima kasih ^_^

Pembuktian Rumus dengan Menggunakan The Geometer’s Sketchpad.

Software geometer’s Sketchpad adalah salah satu software untuk mempermudah guru dalam menjelaskan pembelajaran matematika khususnya pada bidang datar. Berikut tampilan awalnya.

Ubah tampilan menjadi grafik koordinat, caranya dengan mengklik Graph – Grid Form – Square Grid.

Pembuktian Rumus Trapesium.

Langkah-langkahnya:

1.      Buatlah trapesium ABCD sama kaki dengan menggunakan Segment Straightedge Tool.

2.      Beri nama ABCD pada setiap titik dengan menggunakan Text Tool.

3.      Buat garis putus-putus dari titik D dan C yang tegak lurus dengan sisi alas (E) dan (F) dengan menggunakan Segment Straightedge Tool kemudian pada garis tersebut klik kanan – Dashed.

4.      Hubungkan titik D ke F dengan menggunakan Segment Straightedge Tool.

5.      Beri nama garis AE, EF, FB dan DE dengan c, a, c dan t dengan menggunakan Text Tool.

6.      Ketik rumus trapesium dengan menggunakan Text Tool. Luas trapesium adalah jumlah luas persegi panjang + dengan dua kali luas segitiga, maka didapat:

7.      Hitung panjang garis masing-masing AE, EF, BF dan CE dengan klik segment garis kemudian klik kanan – Length.

8.      Hitung masing-masing luas bangun yang ada pada trapesium, dengan menggunakan Polygon pada masing-masing bangun datar, kemudian klik kanan – area. 

9.      Jumlahkan semua luas bangun datar untuk menghasilkan luas trapesium dengan menggunakan Number – Calculate, berikut hasilnya.

10.  Setelah menghitung luas trapesium dengan menjumlahkan semua bangun datar pada trapesium. Sekarang menghitung luas trapesium dengan rumus trapesium (manual) dengan menggunakan Calculate.

11.  Hasilnya seperti dibawah ini. Hasil dari penjumlahan luas bangun datar yang terdapat pada trapesium dengan yang manual ternyata menghasilkan sama.

Pembuktikan Rumus Phytagoras

Langkah-langkah:

1.      Buat segitiga ABC menggunakan segment straightedge tool. 

2.      Klik pada garis untuk mengganti nama dengan cara klik 2 kali pada huruf tersebut.

3.      Buat segitiga yang sama dengan rotasi 90 derajad searah jarum jam.

 

4.      Hubungkan garis a atas dan garis a bawah menggunakan segment straightedge tool.

5.      Klik kanan pada garis penghubung a dan b menggunakan label segment dan beri nama c

6.      Pada segitiga atas lakukan hal yang sama.

7.      Pada segitiga atas beri nama L₁ menggunakan text tool lalu pilih symbolic notation dan pilih subscript

8.      Beri nama L₁ pada segitiga bawah dengan cara yang sama

9.      Beri nama L₂ pada segitiga yang besar dengan cara yang sama

10.  Masukkan rumus trapesium seperti pada gambar di bawah ini

11.  Klik kanan pada masing-masing garis pilih length kemudian kalkulasi angka-angka yang telah di peroleh dengan cara klik number kemudian pilih calculate maka akan terbukti a² + b² = c².

  Membuktikan Jumlah Sudut Dalam Segitiga = 180⁰

Langkah-langkah:

1.      Klik line straightedge tool untuk membuat tiga garis sembarang yang saling berpotongan

2.      Klik 2 garis yang berpotongan kemudian klik construct pilih intersection lakukan pada titik potong yang lain

3.      Klik kanan pada ketiga garis kemudian hide segment

4.      Hubungkan titik-titik dengan segment straight edge tool

5.      Beri nama dengan text tool

6.      Klik titik CAB kemudian klik measure pilih angle, lakukan juga pada sudut ACB, dan sudut ABC setelah ketiga sudut ditemukan klik number pilih calculate maka akan terbukti.

7.      Untuk mengetahui luas segitiganya dengan cara klik poligon klik titik-titiknya, klik kanan pilih area

 

 Sekian, terima kasih.

Trigonometri dengan menggunakan Microsoft Mathematics

Sekarang kita akan menggunakan Microsoft Mathematics dalam pembelajaran trigonometri. Buka aplikasi Micmath-nya lalu pilih trigonometri pada Calculator Pad. Tampilannya seperti dibawah ini.

Sekarang kita akan menyelesaikan penjumlahan pada trigonometri. Caranya dengan mengklik fungsi yang kita inginkan pada Calculator Pad, disini saya akan menghitung sin (90) + cos (45), lalu klik enter. 

Hasilnya terdapat pada worksheet dibawah ini.

Selanjutnya menghitung invers pada trigonometri, misal sin^-1(1) + cos^-1(0).

Hasilnya terdapat pada worksheet dibawah ini.

Sekarang kita akan menghitung integral pada fungsi trigonometri. Caranya dengan mengklik Calculus pada Calculator Pad, lalu pilih lambang integral.

Misal soalnya seperti dibawah ini. Untuk penulisan pangkat tekan shift lalu pilih (^).

Hasilnya terdapat pada worksheet dibawah ini.

Untuk melihat gambar grafik dari fungsi integral tersebut dalam 2 dimensi, tinggal mengklik plot this expression in 2D.

Akan muncul gambar di Graphing dalam bentuk 2 dimensi, seperti dibawah ini.

Atau jika ingin melihat gambar grafik dalam 3 dimensi, caranya kembali ke worksheet kemudian klik plot this expression in 3D.

Hasilnya terdapat pada Graphing seperti dibawah ini.

Sekian, terima kasih.